ASINTOTA OBLICUA

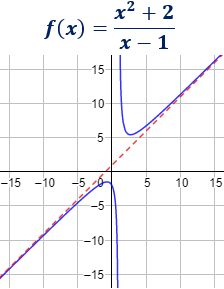
•  La asíntota oblicua de una función f(x) son rectas con ecuación y = px + q que existirán si se cumple que hayan, al menos, uno de estos dos límites:
• 
  
• 
• Necesitamos, en cada caso, saber la ecuación de la recta de cada asíntota oblicua. Hay que averiguar el parámetro p (pendiente de la recta) y el q (punto de corte con el eje de ordenadas).

• En el primer caso, se dice que existe asíntota oblicua por la derecha (o asíntota oblicua en +∞).
• En el segundo caso, se dice que existe asíntota oblicua por la izquierda (o asíntota oblicua en -∞).

El cálculo de la pendiente p se obtiene de uno de estos dos límites:

Dependiendo del valor de p obtenido puede ocurrir que.

1. Si p es un número real diferente de cero, existe asíntota oblicua. Cuando p > 0, la pendiente es positiva y la asíntota va en la dirección del primer al tercer cuadrante de los ejes de coordenadas. Si p < 0, la pendiente es negativa y la asíntota va en la dirección del segundo al cuarto cuadrante.

1. Si el valor de p = ±∞ no existe asíntota oblicua y la rama estudiada es del tipo de la parábola vertical.

1. Si el valor de p = 0; no existe asíntota oblicua y la rama estudiada es del tipo de la parábola horizontal.